J. Reutlinger, L. Glazman, Yu. V. Nazarov, and W. Belzig
Phys. Rev. B 106, 214513 – Published 16 December 2022
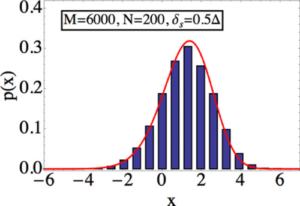ABSTRACT: The energy levels of a quasicontinuous spectrum in mesoscopic systems fluctuate in positions and the distribution of the fluctuations reveals information about the microscopic nature of the structure under consideration. Here, we investigate mesoscopic fluctuations of a secondary gap that appears in the quasiclassical spectrum of a chaotic cavity coupled to one or more superconductors. Utilizing a random matrix model, we compute numerically the energies of Andreev levels and access the distribution of the gap widths. We mostly concentrate on the universal regime E_Th ≫Δ, with E_Th being the Thouless energy of the cavity and Δ being the superconducting gap. We find that the distribution is determined by an intermediate energy scale Δ_g with the value between the level spacing in the cavity
δ_s and the quasiclassical value of the gap E_g. From our numerics we extrapolate the first two cumulants of the gap distribution in the limit of large level and channel number. We find that the scaled distribution in this regime is the Tracy-Widom distribution: the same as found by Vavilov et al. [Phys. Rev. Lett. 86, 874 (2001)] for the distribution of the minigap edge in the opposite limit
E_Th≪Δ. This leads us to the conclusion that the distribution found is a universal property of chaotic proximity systems at the edge of a continuous spectrum in agreement with the known random matrix models featuring a square root singularity in the density of states.