A. Franquet and Yuli V. Nazarov
Phys. Rev. A 100, 062109 – Published 6 December 2019
ABSTRACT: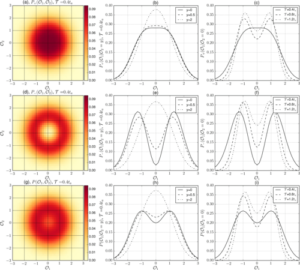
We address the statistics of a simultaneous continuous weak linear measurement of two noncommuting variables on a few-state quantum system subject to a postselected evolution. The results of both postselected quantum measurement and simultaneous monitoring of two noncommuting variables differ drastically from the results of either classical or quantum projective measurement. We explore the peculiarities arising from the combination of the two. We concentrate on the distribution function of two measurement outcomes integrated over a time interval. We formulate a proper formalism for the evaluation of such distribution, and further compute and discuss the resulting statistics for idealized and experimentally relevant setups. We demonstrate the visibility and manifestations of the interference between initial and final states in the statistics of measurement outcomes for both variables in various regimes. We analytically predict the peculiarities at the circle in the distribution of measurement outcomes in the limit of short measurement times and confirm this by numerical calculation at longer measurement times. We demonstrate analytically the anomalously large values of the time-integrated output cumulants in the limit of short measurement times and zero overlap between initial and final states, and give the detailed distributions for this case. We term this situation sudden jump. We present the numerical evaluation of the probability distributions for experimentally relevant parameters in several regimes and demonstrate that interference effects in the postselected measurement can be accurately predicted even if they are small.