Y. Chen and Y. V. Nazarov
Phys. Rev. B 104, 104506 – Published 15 September 2021
Link to arxiv
ABSTRACT: 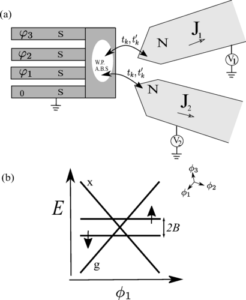A Weyl point in a superconducting nanostructure is a generic minimum model of a topological singularity at low energies. We connect the nanostructure to normal leads thereby immersing the topological singularity in the continuous spectrum of the electron states in the leads. This sets another simple and generic model useful to comprehend the modification of low-energy singularity in the presence of a continuous spectrum. The tunnel coupling to the leads gives rise to new low-energy scale at which all topological features are smoothed. We investigate superconducting and normal currents in the nanostructure at this scale. We show how the tunnel currents can be used for detection of the Weyl point. Importantly, we find that the topological charge is not concentrated in a point but rather is spread over the parameter space in the vicinity of the point. We introduce and compute the resulting topological charge density. We also reveal that the pumping to the normal leads helps to detect and investigate the topological effects in the vicinity of the point.